分角(三角形中的分角定理与张角定理证明)

在三角形ABC中，D是BC上任意一点，设∠BAD=α，∠CAD=β，则有：

分角定理:BD/DC=(AB·sinα)/(AC·sinβ)张角定理:sinα/AC+sinβ/AB=sin(α+β)/AD

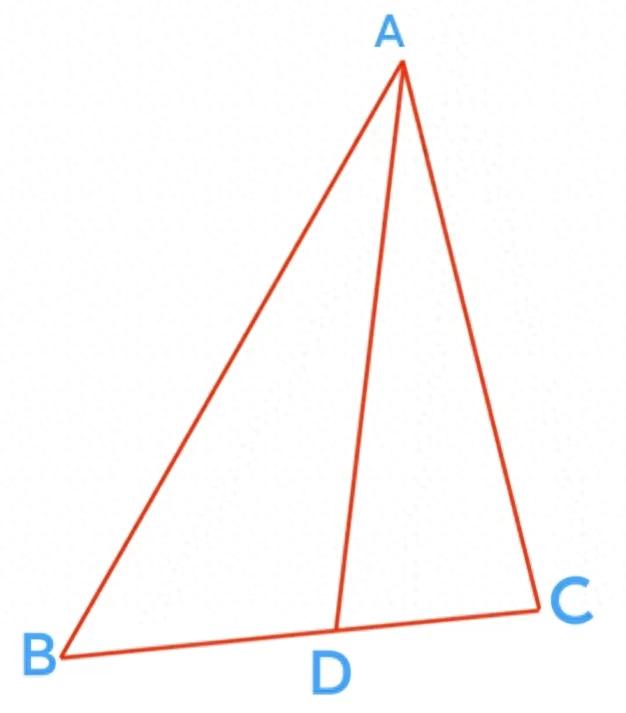
分角定理与张角定理

分角定理证明：因为△ABD与△ADC等高，设其面积分别为S1和S2，则有BD/DC=S1/S2，而S1=AB·AD·sinα，S2=AC·AD·sinβ，将S1、S2代入得：BD/DC=(AB·sinα)/(AC·sinβ)。

两个推论：

1、当AD为∠BAC角分线时，定理变为：BD/DC=AB/AC。

2、当AD为BC边上的中线时，定理变为：AB/AC=sinβ/sinα。

张角定理证明：设△ABC的面积为S，则有S=S1+S2，S=AB·AC·sin(α+β)，S1=AB·AD·sinα，S2=AC·AD·sinβ代入得：

AB·AD·sinα+AC·AD·sinβ=AB·AC·sin(α+β)，两边同除以AB·AC·AD得sinα/AC+sinβ/AB=sin(α+β)/AD。

推论：当AD为∠BAC角分线时，α=β，根据两角和公式sin(2α)=2sinαcosα，定理变为1/AC+1/AB=2cosα/AD。